지난번에 읽은 사경인 회계사의 서적에는 S-RIM이 나온다. 아마 이 글을 읽는 사람들도 S-RIM에 대해 이것저것 궁금해서 찾아보다가 여기에 왔을 것이고, 나도 인터넷에서 여러 글을 읽으며 몇가지 이야기를 읽었다. 초보 주식투자자의 입장에서 S-RIM을 나의 투자법에 적용할 지 안할지 고민해보았다. 이 글의 주제는 다음과 같다.
S-RIM, 과연 나에게 쓸만할까?
지난번에 S-RIM을 이용하여 내가 가진 주식의 주가를 계산해보았는데, 조금 신기한 일이 있었다.
https://corianders.tistory.com/262?category=880129
S-RIM을 활용한 보유 종목 적정 주가 계산
* 본 포스팅은 해당 기업 주식을 매수하거나, 매도하라는 글이 아닙니다. 이미 알려진 정보(신문기사, 공시자료 등)를 바탕으로 기업 상황을 개인적으로 공부한 내용입니다. 모든 정보는 시간을
corianders.tistory.com
첫째로, 현재주가와 큰 차이가 나는 종목이 있다는 것이다. 호텔신라는 S-RIM 결과에 비해 너무나 고평가되었었고 현대차나 기아차는 할인율을 고려하면 오히려 가격이 오르는 현상이 있었기 때문이다. 도대체 S-RIM은 어떤 요소로 구성되어 있고, 특징(장점과 단점)은 무엇일까?
S-RIM이란?
사경인 회계사는 가치 평가 방법이 대략 10여 가지가 있는데 절대·상대가치와 자산·수익가치에 따라 다음으로 나눌 수 있다고 한다.
| 절대가치 | 상대가치 | |
| 자산가치 | NAV | PBR |
| 수익가치 | DCF, EVA, RIM | PER, EV/EBITDA, PSR, PCR |
표로 보니 이때까지 내가 들은 PER, PBR 등은 모두 상대가치법이다. 이와 반대로 책에서 이야기하는 DCF와 RIM은 절대가치법이다. 쉽게 설명하면, 절대가치법으로 계산하면 정확한 적정주가를 알 수 있다. 물론 상한과 하한이 있는 범위로 나온다. 그에 비해 상대가치법은 그 자체로 싸다/비싸다를 알기는 쉽지 않다. 동종업계의 다른 기업을 봐야 상대적으로 비교할 수 있다.
절대가치법은 확실한 가격을 알려주지만 상대가치법에 비해 계산하기 어렵다. 기업의 미래에 많은 가정을 하고, 그 가정을 '정량화' 해야하기 때문이다. 즉, 추정해야 할 변수가 너무 많다. A사의 매출이 몇 퍼센트 성장할까? 그 매출의 얼마가 이익으로 바뀔까? 그렇다면 주가에는 어떻게 반영될까? 이 모든 것을 예측해야 한다. 정확하게 예측할수록 적정주가가 정확해질 것이다.
저자는 부동산시장에서 월세와 전세 변환을 예로 들어 절대 가치법을 설명하고 있다. 만약 전월세 전환율이 6%라면, 전세금 1000만원은 월세 5만원과 동일하다(1000만*6%/12개월). 따라서 보증금 6천/월세40만원짜리 임대물건은 보2천 월60 또는, 전세 1.4억과 (이론상) 동일하다. 이런 계산법이 절대가치법이다.
현금흐름할인법(DCF; Discounted Cash Flow)은 일반적으로 가장 많이 쓰이는 절대가치 평가법이지만 가정할 변수가 너무 많다. 또한 저자는 할인율을 예로 들어 설명하는데, 할인율 산정도 주관적이다보니 이 요소 하나만으로도 기업의 추정폭이 너무 넓어져버리는 단점이 있다. 적정주가가 너무 넓어져버리면 예측에 아무 의미가 없다. 저자 말대로 삼성전자의 적정주가가 2만원에서 20만원이라면 무슨 의미가 있겠는가?
DCF법의 핵심은 현재의 현금흐름을 계산한 뒤, 적절한 할인율로 나누어 이익의 미래가치를 현재가치로 계산한다. 즉, 현재가치 = 연간현금흐름 / 할인율 이다. DCF로 정확히 구하려면 FCF를 정확히 계산하고, 할인율을 정확히 예측해야 한다.
잔여이익모델(RIM; Residual Income Model)은 사경인 회계사의 책에서는 정확하게 나와있지 않으므로 아래의 블로그를 참고했다.
https://m.blog.naver.com/pretty119/220343269789
RIM (잔여이익모델) 밸류에이션 이해하기
주식에 관심이 있으신 분이라면 RIM(Residual Income Model)이라는 가치평가 방법을 들어본 적이 있...
blog.naver.com
RIM계산식은, '가격 = 자기자본 + 잔여이익의 현재가치' 이다.
사경인 회계사는 이를 약간 수정하여 S-RIM을 만들었는데 S는 그의 성을 딴 것으로 보인다. (비꼴 생각은 전혀 없다. 자기 이름붙일 자격은 있다고 본다.)
S-RIM의 식은 다음과 같다.
기업가치 = 자산가치(=자본가치) + 초과이익의 현재가치 = 자기자본 + 초과이익/할인율
= 자기자본 + 자기자본*(ROE - 요구수익률) / 요구수익률 * 할인율=요구수익률
여기서 초과이익(ROE-요구수익률)이 예상과 달리 시간이 지나면서 감소하면 어떻게 될까?
초과이익이 지속하는 정도를 지속계수 ω로 나타내며, 초과이익 유지시 ω=1, 초과이익이 10% 감소시 ω=0.9, 20% 감소시 ω=0.8이 된다. 지속계수(ω)을 식에 반영하면
기업가치 = 자기자본 + 초과이익 * ω / (1 + 요구수익률 - ω)
= 자기자본 + (ROE - 요구수익률) * ω / (1 + 요구수익률 - ω)
이 된다. 이제 이 식에서 대입만 하면 기업의 적정가치를 구할 수 있고 주식수로 나누면 적정주가를 구할 수 있다. 저자가 대입을 추천하는 항목은 아래와 같다.
자기자본 = 최근 지배주주순이익(FnGuide)
ROE = 예상 ROE 사용(FnGuide). 없는 경우 과거 ROE를 통해 산정(추세가 있으면 최근 자료, 없을 경우 3년간 ROE 가중평균)
요구수익률 = 한국신용평가 등급별 금리스프레드의 BBB- 5년만기 회사채 수익률
지속계수 ω = 1, 0.9, 0.8 세가지 모두 대입하여 세 가지 상황을 고려
S-RIM의 구성 요소
S-RIM의 구성요소는 위에서 살펴보았는데 하나씩 생각해보자.
자기자본은 따로 이야기할 것이 없으니 넘어가고, 초보자는 FnGuide의 예상 ROE를 활용하는 것이 좋다고 한다. 사실 이 부분도 해당 업종의 정보를 전업으로 분석하는 사람들이 아니고서는 증권사 애널리스트들의 예상 ROE보다 정확한 예측이 어려울 것 같다.
다음으로 요구수익률. 저자는 BBB-등급의 5년만기 회사채 수익률을 활용한다. 이는 주식투자를 한 이상 이정도의 수익률은 거두어야 한다는 논리이다. BBB- 회사채까지는 투자등급으로 분류가 되고, 그 이하는 투기등급으로 분류한다고 하는데, 이정도까지는 안전성을 가지기 때문에 BBB-로 설정한 듯 하다.
사실 저자는 요구수익률을 "니가 원하는 수익률로 설정해라."라고 한다. 그러나 초보는 말도 안되는 수익률을 상정하는 경우가 많아 대략 5년정도 투자한다는 가정하에 BBB-등급 5년만기 회사채 수익률(이하 B3-)을 활용하였다.
여기서 한가지 문제가 생기는데, 기업가치를 구하는 식에서 초과이익이 음수가 되는 경우다. 예를 들어 B3-가 6.74%일 때, 이보다 낮은 ROE를 보이는 기업(예를 들어 4.42)은 지속계수가 낮아질 때 오히려 기업가치가 증가한다. 음의 값이 커지기 때문이다. 즉, ROE가 해가 지날수록 예상보다 감소하는데도 적정주가는 오르는 기이한 계산결과(4.8만→6.9만)가 나타난다.
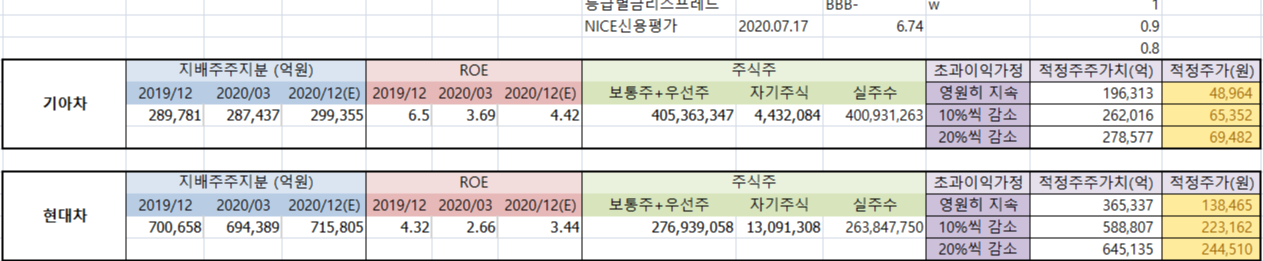
몇가지 값을 더 넣어봐도 계산 결과가 이상하게 나오는 걸 보면, 식 자체가 그렇게 되먹은 것 같다. 어쨌든 저자의 주장도 B3-보다 ROE가 안나오는 기업이라면 그냥 투자하지 않는게 옳을 수도 있다. 생각해보자. 만약 주가가 ROE대로로만 나온다면 B3-보다 낮은 기업에 투자하느니 B3-회사채를 사는게 이득이다.
따라서 자기가 정말 사고 싶은 기업의 ROE가 B3-보다 낮다면 S-RIM이 아닌 다른 방식으로 적정주가를 계산해야 한다. 물론 이런 낮은 ROE가 있는 기업들의 투자가치가 과연 확실한지도 깊이 고민해볼 필요가 있다.
물론 나는 현대차를 샀다 ^.^. S-RIM이 전부는 아니라고 생각하기에...
다음으로 ω(지속계수)를 생각해보자. 만약 기업의 ROE가 해가 지날수록 더 성장하는 경우는 어떻게 될까? 그렇다면 할인율을 1.1이나 1.2로 해야하지 않을까? 혹시나해서 1.1이나 1.2를 넣어보니 제대로 된 결과가 안나왔다. 결국 다항식이니까 지속계수의 변화에 따라 적정주가 그래프를 그릴 수는 있겠지만 중요한 것은 그게 의미가 없다.
기업의 ROE가 늘어나는 상황이 일반적이지 않기 때문이다. 일반적으로 성장하는 기업은 매출과 자본이 증가함에 따라 덩치가 커져서 매년 동일하게 고속성장을 해도 ROE가 조금씩 감소한다. 즉, 그걸 뛰어넘는 순이익을 내는 회사가 일반적인 것은 아니다. 따라서 보수적으로, 가장 최근 발표된 ROE가 유지(ω=1)된다고만 해도 기업이 우량한 성장을 보인다고 말할 수 있다.
즉, ω의 최대치를 1로 두자. 그게 보수적인 접근법이다. 그리고 매년 ROE가 10%씩 감소할 때는 ω=0.9 가 되고,20%감소 시에는 ω=0.8이 된다. 저자는 1, 0.9, 0.8 세 가지 경우로 시뮬레이션을 했는데, 만약 본인이 생각하기에 이 회사가 가파르게 ROE가 하락할 것이라고 생각한다면 0.7이나 0.5를 대입해도 될 것이다. 다만 이렇게 예상하려면 근거가 있어야 할텐데, "난 특별히 더 보수적으로 적정주가를 계산해서 방어적으로 투자할거야"라는 사람이 아니면 따로 수정할 필요는 없어보인다. 시뮬레이션을 통해서 "ROE가 이만큼 줄어도 이정도 가격에선 적정하겠군"이라고 참고만 하면 될 듯 하기 때문이다. ROE의 20%하락만해도 큰 수치라고 생각한다. 20에서 20%하락하면 16으로 줄어든다.
자 그렇다면 이제 B3-를 기준으로 각종 변수(요구수익률과 지속계수 등)를 조정할때 적정주가가 어떻게 바뀔지 생각해보자.
요인 변화에 따른 S-RIM 변화
1. 적정주가 변화에 따른 우리의 전략
만약 S-RIM을 구성하는 특정 지표가 변한다면 우리는 어떻게 대응해야 할까? 예를 들어 새 보고서가 나오면서 기업이 극적으로 턴어라운드하며 ROE가 바뀐다든지, B3-(BBB- 등급 회사채 5년만기 수익률)가 큰 폭으로 변한다든지, 지속계수를 좀 더 조정해보겠다고 했을 때 말이다. 사경인 회계사의 추천 매매전략은 다음과 같다. 참고로 ω를 바꾸는 게 아니라, 현재 회사의 주가가 각 ω에 따른 S-RIM 적정주가에 도달했을 때 대응전략을 의미한다.
| 현재주가 | 대응전략 | 비고 |
| ω=0.8 계산값 이하 | 비교적 싸므로 매수 | |
| ω=0.8 과 ω=0.9 사이 | 보류 (적정가격) | |
| ω=0.9 계산값 이상 | 주식의 1/3 매도 | |
| ω=1 | 1/3 추가 매도 | 남은 수량은 지켜본 뒤 매도 |
우리가 어떤 기업의 주식을 살 때, S-RIM으로 계산된 적정주가보다 낮은 가격에서 매수하길 원하고 현재주가가 적정주가보다 높을 때(또는 단기간에 빨리 높아질 때) 매도하면 최대의 이익을 얻는다.
그렇다면 S-RIM으로 계산해보니 세 적정주가가 현재주가보다 전반적으로 모두 높다면 어떻게 생각할까? 생각보다 현재주가가 엄청싸니까(=시장에서 저평가) 많이 사야겠다고 결정한다. 그리고 조금씩 오르든내리든 현재주가가 ω=0.9~1일 때 적정주가에 도달할 때까지 보유하고 있을 것이다.
S-RIM 계산 결과 세 적정주가가 현재주가보다 모두 낮다면, 즉 내가 사려고 고려했던 회사가 고평가되었다는 것을 알면 매수를 주저할 것이다. 이미 한계점에 도달했다고 여길 것이고, 만약 가진 물량도 매도할 것이다.
정리하면 정확히 계산되었다는 전제하에 S-RIM적정주가(ω=0.8) > 현재주가 일 때 최상의 매수타이밍이다. S-RIM적정주가(ω=1) < 현재주가 일 때 최상의 매도타이밍이다.
내가 아직 주식을 사지 않았다면 조사하는 회사의 S-RIM 적정주가는 높을수록 좋다. 그만큼 살만한 가치가 있는 회사다.
이제 다시 변수를 생각해보자.
1. 요구수익률을 낮출 때
예를 들면 5년만기가 아닌 1년 만기라고 생각한다면? 아니면 A+ 등급이라고 생각한다면? 내 요구수익률을 줄이면 S-RIM으로 계산한 기업의 적정주가는 일반적으로 증가한다. 즉, 내가 주식투자로 벌어들일 수익의 기대치를 낮출수록 S-RIM으로 계산한 적정주가는 높아지면서, 시장에서 더 많은 기업을 "살만하다"라고 평가하는 것이다. 눈을 낮춰서 조금만 벌면 된다고 결정하면 도처에 살만한 기업이 널려있는 셈이다. 물론, 내 요구수익률을 낮춘 결과이므로 실제 기업의 주가가 오를지 내릴지는 알 수 없다.
2. 요구수익률을 높일 때
반대로 요구수익률을 B3-보다 높인다고 가정해보자. 요구수익률을 높일수록 S-RIM으로 계산한 기업의 적정주가는 낮아진다. 따라서 현재주가와 S-RIM으로 계산한 적정주가의 차이가 적어지거나, 오히려 현재주가가 S-RIM적정주가보다 높아지게 되면서 우리가 매수할만한 기업의 수는 적어진다. 즉, 시장에서 매수할만큼 매력적으로 보이는 회사가 줄어들고 이미 산 것도 온통 매도해야만 할 것처럼 보인다. 한가지 주의해야 할 점은 위에서 말한 것 처럼 요구수익률이 ROE보다 높을 경우, 지속계수(ω)가 낮아짐에도 적정주가는 오르는 식의 오류가 생길 수 있다. 이 말은 어떤 회사의 ROE보다 요구수익률이 높을 경우 그 회사에 투자하지말고 요구수익률을 낼 수 있는 투자수단(낮은 등급의 회사채)에 투자해야한다는 것이다.
아무튼 요구수익률을 높인다면 우리가 투자할만한 회사의 범위를 줄일 수는 있다. 또한 실제로 회사의 주가가 적정주가만큼 낮아진다는 것도 아니고, 조금만 올라도 충분히 올랐다고 판단하므로 현재 주가를 좀 더 방어적으로 평가하게 된다. 물론 충분히 더 오를 수 있음에도 팔아버리는 경우도 생길 것이다.
3. 지속계수를 낮출 때
지속계수(ω)는 세 가지 수치를 사용한다. 그 이유는 위에서 말한것처럼 회사가 꾸준히 일정하게 성장한다고 가정하더라도 덩치가 커지며 ROE는 낮게 나타나기 때문이다. ROE가 일정하려면, 예상보다 훨씬 더 큰 이익을 내야 한다. 따라서 지속계수 ω=1 인 가정 자체가 회사의 ROE 전망을 긍정적으로 평가한 것이다. 대개의 회사는 ROE가 어느 정도는 감소하기 때문에 ω를 이용하여 RIM식을 보정하는 것이다. 사경인 회계사는 초과이익이 계속해서 지속되서 이상적인 경우를 ω=1, 매년 10% 감소하는 경우를 ω=0.9, 20%씩 감소하는 경우를 ω=0.8로 두고, 위의 표와 같이 현재주가가 ω=0.8 일때 적정주가 이하인 경우 매수하는 것이 좋다고 한다. 주의해야 할 것은 모든 기업이 기본값이 ω=1이 아니라는 것이다. 기업의 미래를 알 수 없으므로 최선을 다해 성장하는 기업의 ROE도 자연스럽게 20%정도는 떨어질수도 있다고 가정하는 것 뿐이다. 따라서 지속계수 세가지를 이용한 S-RIM의 세가지 적정주가는 최상의 상황(가정1), 꽤 좋은 상황(가정2), 적당히 좋은(?) 상황(가정3)을 가정한 것이라고 할 수 있다.
만약 어떤 업종(또는 시장)의 미래가 지속적으로 낮아진다면 S-RIM에서 개별기업의 ROE를 조정해도 되겠지만 지속계수를 수정하는 것도 한가지 방법일 것이다.
만약 ω에 더 낮은 수치를 넣는다면 당연히 적정주가는 내려가게 된다. 그런데 ω는 세 가지가 있어서 세가지 가정에 어떤 것을 넣냐에 따라 다른 결과가 나온다. 먼저 가정1(최상의 성장 상태)에서 ω를 낮추면 기업의 적정주가는 내려가므로 얼른 팔아야 할 매물로 보인다. 즉 상황을 비관적(방어적)으로 보는 것이다. 마찬가지로 가정3의 ω를 더 낮추면 적정주가가 낮아져서 현재주가가 적정주가보다 낮더라도 큰 차이가 안나게 되어 매수를 주저하게 된다. 즉, 지속계수를 낮출수록 주가를 더 방어적으로 보면서, 매수할만한 기업의 폭이 줄어들게 된다. 요구수익률과 같은 상황으로, 적정주가가 낮아질수록 방어적으로 투자할 수 있지만, 반대로 이익을 볼 확률도 줄게 된다.
그렇다면 지속계수를 권고(1, 0.9, 0.8)보다 높이는건 어떤가?
결론부터 말하면 별로 좋은 선택은 아니다. 1보다 높은 경우 S-RIM이 제대로 된 결과를 내지 않는다. 신뢰성이 없다. 또한 기업의 일생으로 봤을 때도, ROE가 증가하는 미래는 굉장히 낙관적으로 보는 상황이므로 ROE가 영원히 유지된다고 보는 것(ω=1)이 최선의 가정이다. 조금씩 감소(0.9, 0.8) 하는 폭을 줄일 수는 있지만 해당 업종이나 사이클에서의 평균적인 ROE의 감소분을 정확히 알고있거나, 예측할 수 없다면 섣불리 건드리지 않는 것이 좋을 것이다.
4. ROE를 조정할 때
만약 내가 보고 있는 기업의 ROE가 오른다면? 또는 유망한 줄 알고 투자를 했는데 ROE가 내려간다면 어떻게 해야할까. 일반적으로 ROE가 올라갈수록 적정주가는 상승한다. 당연한 이치다. 돈 잘 버는 회사니까 적정주가가 올라가지 않겠는가. 문제는 ROE가 떨어지는 상황인데, 만약 ROE가 요구수익률보다 낮아지면 S-RIM을 쓸 수 없다. 식에 음수가 나오면서 ω가 감소할수록 적정주가가 높아지기 때문이다. 따라서 ROE를 조정할 때는 요구수익률 이하로는 조정하지말자.
한가지 의문점은 ROE가 요구수익률보다 낮더라도, ω=1일 때의 가치는 의미가 있을 것이라는 점이다. 당연히 초과이익이 아닌 초과손실이 있다면 주가에 마이너스로 반영이 되서 적정주가가 낮아질텐데... 따라서 ω=1일때의 값은 의미가 있을텐데, ω<1이 된다면 적정주가가 오히려 증가한다는 점이다. 그 때는 할인율개념이 아니라 ROE가 오히려 ω의 역수만큼 성장한다는 의미인가? 식의 유도를 제대로 이해하지 못해서 정확히 이해는 안 된다.
또한 S-RIM의 계산의 근본은 결국 자본총계(지배주주지분)과 ROE에 있다. 만약 ROE로 평가하기 어려운 기업들, 예컨대 지금은 돈을 못 벌고 있지만 앞으로 미래에 돈을 많이 벌 것 같은 기업들은 S-RIM으로 평가하기 어렵다. 또는 무형자산처럼 재무제표 상에 제대로 기재가 안되어 있는 부분이 많은 기업도 S-RIM사용해야 할 것이다. S-RIM이 ROE에 큰 영향을 받는다는 건 인터넷 검색을 통해서도 확인했다.
https://www.clien.net/service/board/cm_stock/14820646
사경인 회계사는 SRIM을 잘못이해하고 있네요. : 클리앙
사경인 회계사는 "재무제표 모르면 주식투자 절대로 하지 마라"에서 기업가치를 어떻게 산정하는지에 대한 단순하고 직관적인 척도로 SRIM이라는 걸 제안했는데요. 식을 잘 보면, 자기자본 term이
www.clien.net
위의 글에 댓글을 적진 않았지만, 여기서 반론을 해본다면 위 글의 저자의 말이 틀린 것은 아닌데 책의 저자(사경인 회계사)가 굳이 식을 정리하지 않은 이유는 분모의 할인율(또는 요구수익률, Ke)에 지속계수(ω)를 넣기 위해서라고 생각한다. ROE가 지속적으로 감소하므로
기업가치=자기자본 + 초과이익 * 1 / 할인율
에서 할인율 항을 ω / (1+할인율-ω) 로 바꾸었다. 따라서 클리앙 글에서처럼 단순히 약분되지는 않는다.
또한, S-RIM의 가정이 ROE의 감소시간이 무한대로 설정되어 있는 점인데, 이런점을 개선한 사람도 있는 듯해서, 대단해서 링크를 올려둔다.
S-RIM 수식을 보다 정밀하게 해보자!
사경인 회계사님의 S-RIM 방법은 매우 좋은 방법이라 생각된다. 주식에 있어서 가치를 판단하는 것은 수직적 가치 투자자들에게 있어서 큰 이슈 중 하나이기 때문이다. 그것을 나와 같은 일반인��
made-by-tia.tistory.com
정리
정리해보자면, S-RIM을 이용한 적정주가는 ROE가 높을수록, 지속계수(ω)가 1에 근접할수록, 요구수익률(할인율)을 낮출수록 증가한다. 또한 ROE가 요구수익률보다 낮은 경우 식의 값이 제대로 나오지 않으므로 주의해야 한다.
'주식' 카테고리의 다른 글
| 지금이라도 주식 더 매수해야할까? 2021년 주가에 대한 고찰 (0) | 2021.01.10 |
|---|---|
| 초보자가 미국 국채 쉽게 매매하는 방법 : ETF로 매매하기 (0) | 2021.01.09 |
| 피터 린치의 투자법에 대한 단상 (0) | 2020.08.02 |
| S-RIM을 활용한 보유 종목 적정 주가 계산 (0) | 2020.07.19 |
| 연결재무제표 쉽게 이해하기 (0) | 2020.07.08 |